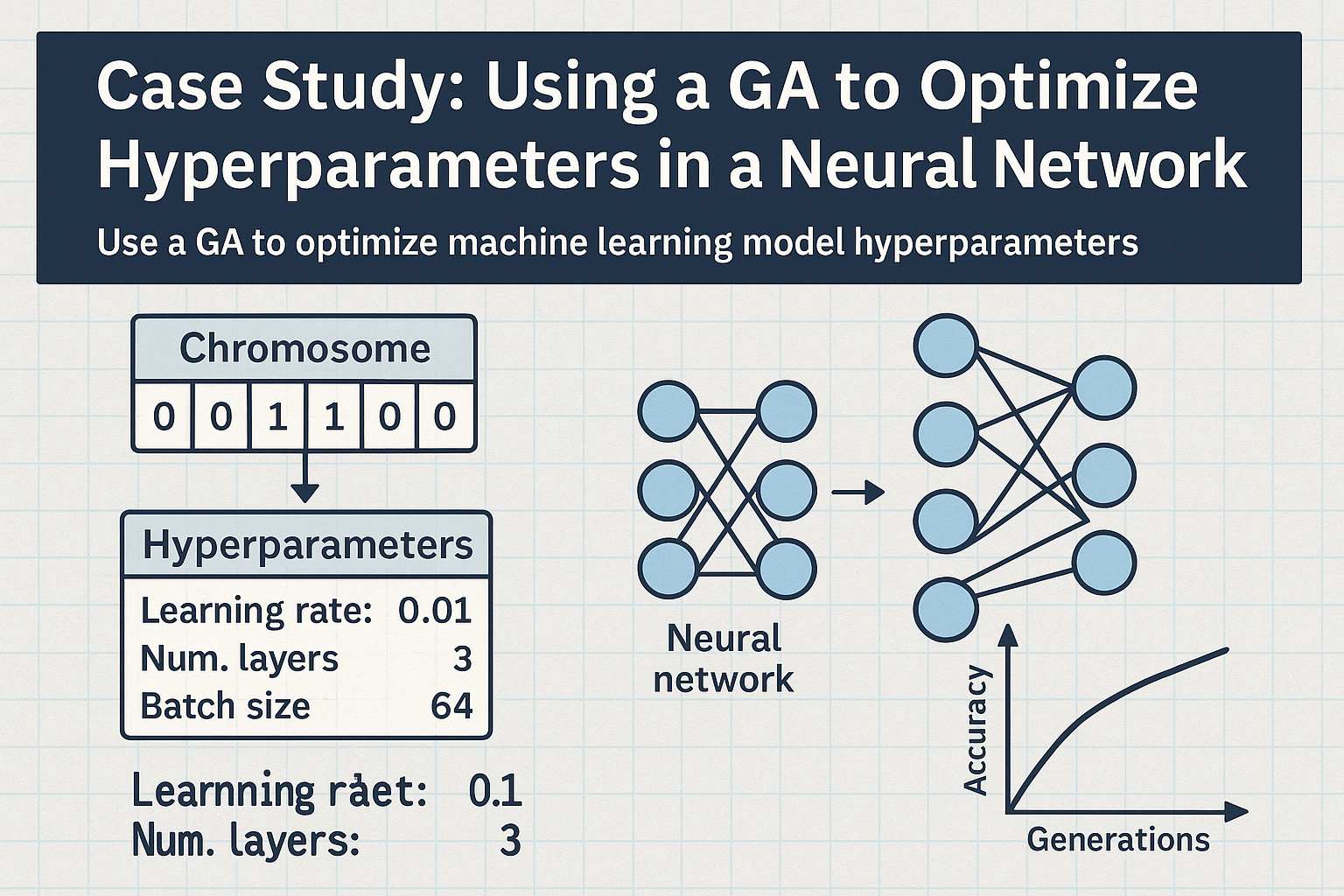
Day 33: Case Study: Using a Genetic Algorithms to Optimize Hyperparameters in a Neural Network
- Chris Woodruff
- September 16, 2025
- Genetic Algorithms
- .NET, ai, C#, dotnet, genetic algorithms, programming
- 0 Comments
Tuning hyperparameters for machine learning models like neural networks can be tedious and time-consuming. Traditional grid search or random search lacks efficiency in high-dimensional or non-linear search spaces. Genetic Algorithms (GAs) offer a compelling alternative by navigating the hyperparameter space with adaptive and evolutionary pressure. In this post, we’ll walk through using a Genetic Algorithm in C# to optimize neural network hyperparameters using a practical example.
The Optimization Problem
Let’s say you have a simple feedforward neural network built with ML.NET or a custom framework. Your goal is to find the best combination of the following hyperparameters:
- Number of hidden layers (1 to 3)
- Neurons per layer (10 to 100)
- Learning rate (0.0001 to 0.1)
- Batch size (16 to 256)
Each combination impacts the training accuracy and performance of the model. Using a GA, we encode each hyperparameter into a gene and build chromosomes representing complete configurations.
Chromosome Design
We can define a chromosome as a list of parameters:
public class HyperparameterChromosome
{
public int HiddenLayers { get; set; } // [1-3]
public int NeuronsPerLayer { get; set; } // [10-100]
public double LearningRate { get; set; } // [0.0001 - 0.1]
public int BatchSize { get; set; } // [16 - 256]
public double Fitness { get; set; }
}
A random generator function initializes a diverse population:
public static HyperparameterChromosome GenerateRandomChromosome()
{
Random rand = new();
return new HyperparameterChromosome
{
HiddenLayers = rand.Next(1, 4),
NeuronsPerLayer = rand.Next(10, 101),
LearningRate = Math.Round(rand.NextDouble() * (0.1 - 0.0001) + 0.0001, 5),
BatchSize = rand.Next(16, 257)
};
}
Fitness Function: Model Evaluation
We define fitness based on validation accuracy from training the neural network using the encoded hyperparameters. To save time during this example, we simulate the evaluation step with a mocked accuracy function:
public static double EvaluateChromosome(HyperparameterChromosome chromo)
{
// Simulate evaluation for example purposes
double accuracy =
0.6 +
(0.1 * (chromo.HiddenLayers - 1)) +
(0.001 * chromo.NeuronsPerLayer) -
Math.Abs(chromo.LearningRate - 0.01) +
(0.0001 * chromo.BatchSize);
chromo.Fitness = accuracy;
return accuracy;
}
In a real-world case, you’d integrate this with a training loop using a machine learning library and compute validation accuracy.
Genetic Operators
Use standard crossover and mutation mechanisms. For simplicity, we’ll implement single-point crossover and bounded random mutation:
public static (HyperparameterChromosome, HyperparameterChromosome) Crossover(HyperparameterChromosome p1, HyperparameterChromosome p2)
{
return (
new HyperparameterChromosome
{
HiddenLayers = p1.HiddenLayers,
NeuronsPerLayer = p2.NeuronsPerLayer,
LearningRate = p1.LearningRate,
BatchSize = p2.BatchSize
},
new HyperparameterChromosome
{
HiddenLayers = p2.HiddenLayers,
NeuronsPerLayer = p1.NeuronsPerLayer,
LearningRate = p2.LearningRate,
BatchSize = p1.BatchSize
}
);
}
public static void Mutate(HyperparameterChromosome chromo)
{
Random rand = new();
int geneToMutate = rand.Next(0, 4);
switch (geneToMutate)
{
case 0:
chromo.HiddenLayers = rand.Next(1, 4);
break;
case 1:
chromo.NeuronsPerLayer = rand.Next(10, 101);
break;
case 2:
chromo.LearningRate = Math.Round(rand.NextDouble() * (0.1 - 0.0001) + 0.0001, 5);
break;
case 3:
chromo.BatchSize = rand.Next(16, 257);
break;
}
}
GA Loop
The core loop evaluates the population, selects parents, applies crossover and mutation, and evolves across generations.
int populationSize = 50;
int generations = 30;
double mutationRate = 0.1;
List<HyperparameterChromosome> population = Enumerable.Range(0, populationSize)
.Select(_ => GenerateRandomChromosome())
.ToList();
for (int gen = 0; gen < generations; gen++)
{
foreach (var chromo in population)
EvaluateChromosome(chromo);
population = population.OrderByDescending(c => c.Fitness).ToList();
List<HyperparameterChromosome> newPopulation = new List<HyperparameterChromosome>();
while (newPopulation.Count < populationSize)
{
var parent1 = TournamentSelect(population);
var parent2 = TournamentSelect(population);
var (child1, child2) = Crossover(parent1, parent2);
if (new Random().NextDouble() < mutationRate) Mutate(child1);
if (new Random().NextDouble() < mutationRate) Mutate(child2);
newPopulation.Add(child1);
newPopulation.Add(child2);
}
population = newPopulation;
Console.WriteLine($"Gen {gen}: Best Accuracy = {population[0].Fitness:F4}");
}
Tournament Selection
A common selection method that balances performance and diversity:
public static HyperparameterChromosome TournamentSelect(List<HyperparameterChromosome> population, int tournamentSize = 5)
{
Random rand = new();
var competitors = population.OrderBy(_ => rand.Next()).Take(tournamentSize).ToList();
return competitors.OrderByDescending(c => c.Fitness).First();
}
Results and Use Cases
When integrated with real neural network training, this GA framework can intelligently explore the hyperparameter landscape. It adapts based on feedback and converges toward high-performing configurations over time.
This approach is especially useful when:
- The search space is non-continuous or complex
- Training time is expensive and gradient-free optimization is preferred
- Combinatorial parameter dependencies exist
GAs will not replace traditional optimizers for every use case, but they can offer robustness and simplicity when tuning difficult or poorly-behaved models.
In the next post, we will look at integrating GA-based hyperparameter tuning into an ML pipeline using automated tools and reporting.






