Day 23: Introduction to Non-dominated Sorting Genetic Algorithm II (NSGA-II) in C#

Day 23: Introduction to Non-dominated Sorting Genetic Algorithm II (NSGA-II) in C#

Chris Woodruff
August 12, 2025
Genetic Algorithms
.NET, ai, C#, dotnet, genetic algorithms, programming
0 Comments

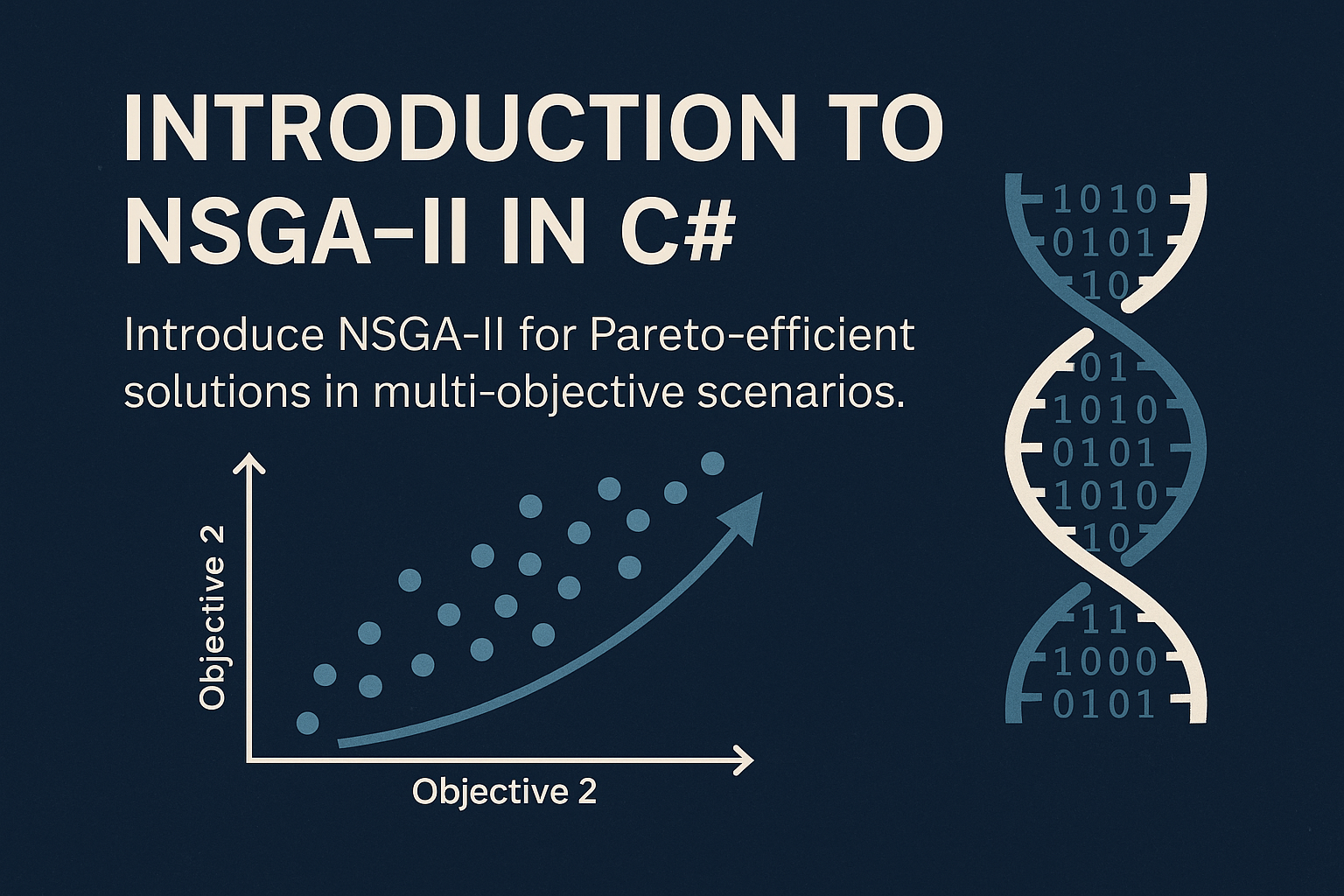
As we extend our use of genetic algorithms (GAs) beyond single-objective problems, we enter the realm of multi-objective optimization, where trade-offs must be made between competing goals. The Non-dominated Sorting Genetic Algorithm II (NSGA-II) is one of the most widely used algorithms for solving such problems. Its design maintains a diverse population of high-quality solutions that form what is known as a Pareto front.

In this post, we will explore the core ideas of NSGA-II and walk through a simplified implementation in C# that demonstrates non-dominated sorting and diversity preservation using crowding distance.

Why NSGA-II?

Traditional GAs work well when you have a single fitness function. But when multiple objectives must be optimized simultaneously, combining them into a single scalar value often leads to suboptimal solutions. NSGA-II addresses this by:

Sorting individuals based on Pareto dominance
Promoting diversity using a crowding distance metric
Preserving elite solutions without duplication or bias

The result is a collection of solutions that approximate the optimal trade-offs across objectives.

Key Components of NSGA-II

Non-dominated Sorting: Individuals are ranked based on dominance. The first front contains solutions that are not dominated by any others. The second front contains individuals dominated only by those in the first front, and so on.
Crowding Distance: Within each front, individuals are scored based on how far they are from others in objective space. This ensures that the final population maintains diversity.
Selection: When forming the next generation, individuals are selected based on front rank and crowding distance.

Chromosome Structure

We define a multi-objective chromosome with two objectives:

public class Chromosome
{
    public int[] Genes { get; set; }
    public double Objective1 { get; set; }
    public double Objective2 { get; set; }
    public int Rank { get; set; }
    public double CrowdingDistance { get; set; }

    public void Evaluate()
    {
        Objective1 = Genes.Sum(); // Dummy objective
        Objective2 = Genes.Length - Objective1; // Second objective as complement
    }
}

Non-dominated Sorting

We group individuals into fronts using Pareto dominance.

public static List<List<Chromosome>> NonDominatedSort(List<Chromosome> population)
{
    var fronts = new List<List<Chromosome>>();
    var dominationCounts = new Dictionary<Chromosome, int>();
    var dominated = new Dictionary<Chromosome, List<Chromosome>>();

    var front = new List<Chromosome>();

    foreach (var p in population)
    {
        dominated[p] = new List<Chromosome>();
        dominationCounts[p] = 0;

        foreach (var q in population)
        {
            if (Dominates(p, q))
                dominated[p].Add(q);
            else if (Dominates(q, p))
                dominationCounts[p]++;
        }

        if (dominationCounts[p] == 0)
        {
            p.Rank = 1;
            front.Add(p);
        }
    }

    fronts.Add(front);

    int rank = 1;
    while (fronts[rank - 1].Count > 0)
    {
        var nextFront = new List<Chromosome>();
        foreach (var p in fronts[rank - 1])
        {
            foreach (var q in dominated[p])
            {
                dominationCounts[q]--;
                if (dominationCounts[q] == 0)
                {
                    q.Rank = rank + 1;
                    nextFront.Add(q);
                }
            }
        }
        fronts.Add(nextFront);
        rank++;
    }

    return fronts;
}

public static bool Dominates(Chromosome a, Chromosome b)
{
    bool betterInAny = false;

    if (a.Objective1 < b.Objective1) betterInAny = true;
    else if (a.Objective1 > b.Objective1) return false;

    if (a.Objective2 < b.Objective2) betterInAny = true;
    else if (a.Objective2 > b.Objective2) return false;

    return betterInAny;
}

Crowding Distance Calculation

After sorting, we calculate the crowding distance within each front:

public static void AssignCrowdingDistance(List<Chromosome> front)
{
    int count = front.Count;
    if (count == 0) return;

    foreach (var c in front)
        c.CrowdingDistance = 0;

    foreach (var objectiveSelector in new Func<Chromosome, double>[] { c => c.Objective1, c => c.Objective2 })
    {
        var sorted = front.OrderBy(objectiveSelector).ToList();
        sorted[0].CrowdingDistance = double.PositiveInfinity;
        sorted[^1].CrowdingDistance = double.PositiveInfinity;

        double min = objectiveSelector(sorted[0]);
        double max = objectiveSelector(sorted[^1]);
        double range = max - min;

        if (range == 0) continue;

        for (int i = 1; i < count - 1; i++)
        {
            double prev = objectiveSelector(sorted[i - 1]);
            double next = objectiveSelector(sorted[i + 1]);
            sorted[i].CrowdingDistance += (next - prev) / range;
        }
    }
}

Selection for the Next Generation

Individuals are selected from fronts, starting from the best (lowest rank). If a front overflows the population limit, we use crowding distance to fill the remaining slots.

public static List<Chromosome> SelectNextGeneration(List<List<Chromosome>> fronts, int populationSize)
{
    var newPopulation = new List<Chromosome>();

    foreach (var front in fronts)
    {
        AssignCrowdingDistance(front);
        if (newPopulation.Count + front.Count <= populationSize)
        {
            newPopulation.AddRange(front);
        }
        else
        {
            var sorted = front.OrderByDescending(c => c.CrowdingDistance);
            newPopulation.AddRange(sorted.Take(populationSize - newPopulation.Count));
            break;
        }
    }

    return newPopulation;
}

Conclusion

NSGA-II brings structure and power to multi-objective genetic algorithms by combining dominance-based ranking and diversity preservation. Implementing NSGA-II in C# enables developers to tackle real-world problems with conflicting goals and identify a set of trade-off solutions that would be missed by single-objective approaches.

In the next post, we will look at scaling these algorithms across threads and machines to make them production-ready.

You can find the code demos for the GA series at https://github.com/cwoodruff/genetic-algorithms-blog-series

Tags: .NET ai C# dotnet genetic algorithms programming