Day 12: Genetic Algorithms’ Elitism for Evolution Survival of the Fittest

Natural selection favors the survival of the fittest, but evolution in the wild is not always efficient. In genetic algorithms, we can bias the process toward faster convergence by deliberately preserving top-performing individuals across generations. This technique is known as elitism, and it is one of the simplest yet most effective strategies for enhancing GA performance.

Today’s post focuses on applying elitism in a C# genetic algorithm to ensure that the best solutions are never lost. We will define elitism, explain its impact on the evolutionary process, and demonstrate how to implement it cleanly and effectively.

What Is Elitism?

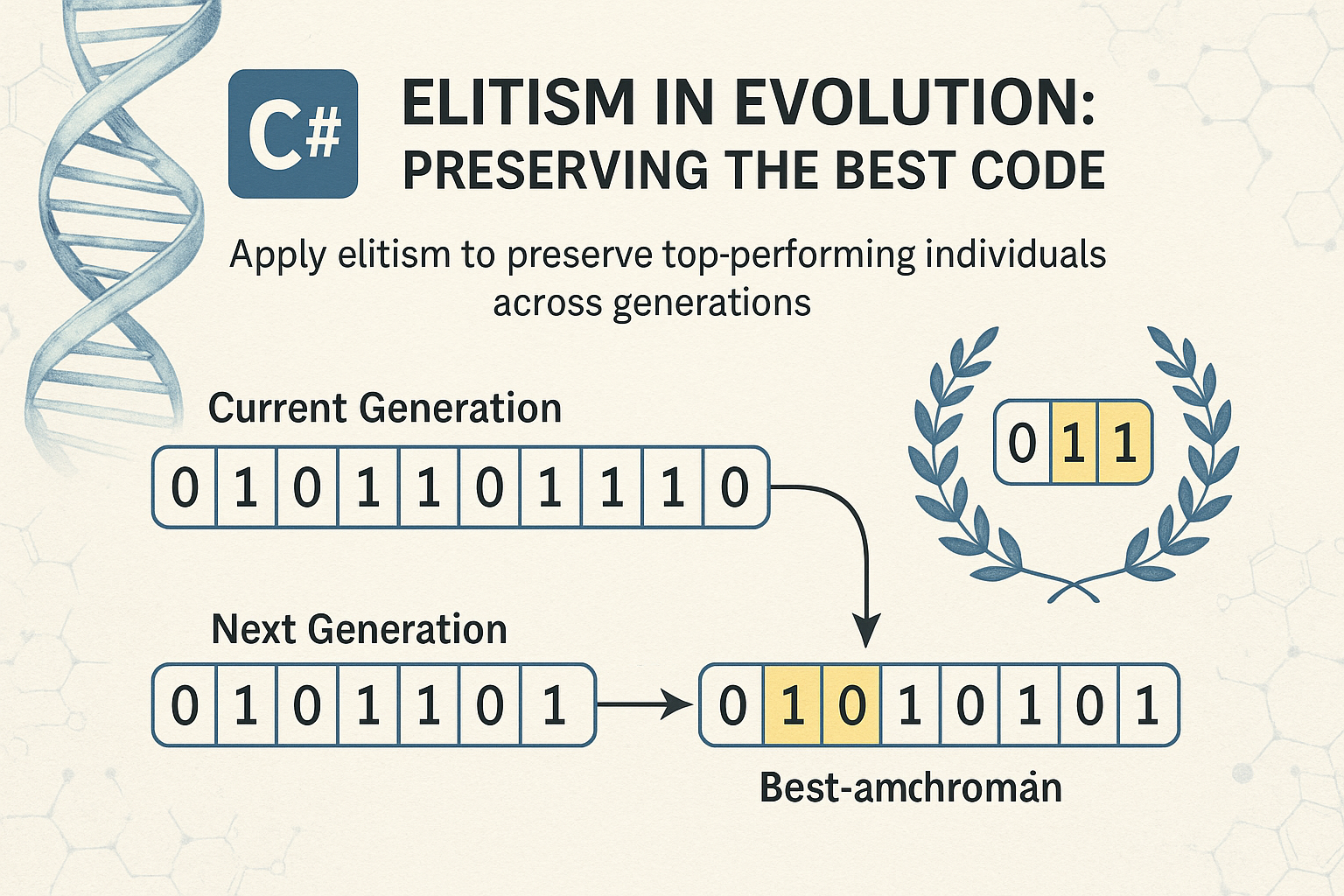
Elitism is a selection method that guarantees a specific number of the fittest chromosomes (called elites) are carried over unchanged from one generation to the next. These elite individuals bypass crossover and mutation to preserve their exact structure and performance.

Without elitism, there’s always a chance that recombination or mutation degrades even the best solutions. Elitism avoids this risk by protecting a small number of high-quality chromosomes.

Why Use Elitism?

• Preserves High Fitness: Ensures top solutions are passed down through the gene pool.
• Accelerates Convergence: Reduces the time to reach acceptable solutions.
• Stabilizes Evolution: Maintains a performance baseline during exploration.

However, overuse of elitism can reduce diversity and lead to premature convergence. It’s best used in moderation, typically preserving 1 to 5 of the best individuals per generation.

Implementing Elitism in C#

Assume you have a List<Chromosome> representing the current population. Here’s how to apply elitism to extract the top-performing chromosomes:

public List<Chromosome> ApplyElitism(List<Chromosome> population, int eliteCount)
{
    return population
        .OrderByDescending(c => c.FitnessScore)
        .Take(eliteCount)
        .Select(c => new Chromosome((char[])c.Genes.Clone()))
        .ToList();
}

This implementation:

• Sorts the population by fitness
• Takes the top eliteCount chromosomes
• Clone them to avoid reference issues when evolving the next generation

You can then insert these elites directly into the next generation before filling the remaining slots via selection and crossover.

Integrating Elitism in the GA Loop

Below is a simplified structure of how elitism fits into your main evolution logic:

var newPopulation = new List<Chromosome>();

// Step 1: Elitism
var elites = ApplyElitism(currentPopulation, eliteCount);
newPopulation.AddRange(elites);

// Step 2: Fill the rest of the population
while (newPopulation.Count < populationSize)
{
    var parent1 = TournamentSelection(currentPopulation);
    var parent2 = TournamentSelection(currentPopulation);

    var child = parent1.Crossover(parent2);
    child.Mutate(mutationRate);
    newPopulation.Add(child);
}

This ensures that elite individuals are always preserved, while the rest of the population is subject to natural selection or evolutionary pressure.

Choosing an Elitism Strategy

Population Size	Typical Elite Count
50	1–2
100	2–5
500+	5–10

You can also apply a dynamic elitism strategy, where the number of elites changes based on population diversity or progress in generations.

Caution: Elitism vs. Diversity

Elitism introduces exploitation pressure. If used excessively, it can crowd out diversity and lead to genetic stagnation. To avoid this:

• Keep elite count low
• Combine with mutation or diversity-preserving selection
• Monitor convergence rates and diversity metrics

Conclusion

Elitism is a powerful addition to your genetic algorithm, ensuring that hard-won solutions are not lost in the randomness of evolution. Used properly, it stabilizes progress and improves your algorithm’s performance with reduced volatility.

Up Next

In the next post, we’ll integrate all operator components —selection, crossover, mutation, and elitism —into a configurable GA loop. You’ll learn how to set population size, mutation rate, elite count, and generation limits to adapt your GA to different problem domains.

You’ve built the parts. Now it’s time to engineer the machine.